Materi trigonometri merupakan salah satu materi membingungkan dalam pelajaran matematika. Memang kesulitan dalam mengerjakan soal trigonometri pasti ada. Mengerjakan soal trigonometri terkadang cepat, terkadang lambat. Rumus saja tidaklah cukup untuk mengerjakan soal trigonometri, kita butuh IDE, bagaimana langkah yang kita ambil selanjutnya. Untuk mendapatkan ide tidaklah mudah, butuh banyak pengalaman seperti banyak latihan mengerjakan soal-soal trigonometri.
maka dari itu janganlah cepat putus asa dalam mengerjakan soal terutama trigonometri, karena putus asa tidak dapat membuat anda sukses.
Kita lanjut ke materi trigonometri
Yang perlu diingat adalah IDENTITAS TRIGONOMETRI
1. sin 2 x + cos2 x = 1
2. 1 + tan2 x = sec2 x
3. 1 + cotan2 x = cosec2 x tinggal tambah awalan co- saja. Tidak perlu susah-susah.
kemudian hubungan antara sin cos tan dengan cosec sec cotan
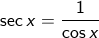 boleh ditulis cosec x
boleh ditulis cosec x
kemudian hubungan antara sin cos tan dengan cosec sec cotan
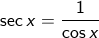 boleh ditulis cosec x
boleh ditulis cosec xboleh ditulis cotan x atau ctg x
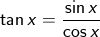.gif)
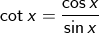.gif)
karena tan x merupakan kebalikan atau invers dari cot x
Sekarang bagaimana cara menghafal sudut-sudut yang berelasi ?
sin ( 90 - a ) = cos a cos ( 90 - a ) = sin a tan ( 90 - a ) = cot a cot ( 90 - a )= tan a | sin ( 90 + a ) = cos a cos ( 90 + a ) = -sin a tan ( 90 + a ) = -cot a cot ( 90 + a )= -tan a |
sin ( 180 - a ) = sin a cos ( 180 - a ) = -cos a tan ( 180 - a ) = -tan a cot ( 180 - a )= -cot a | sin ( 180 + a ) = -sin a cos ( 180 + a ) = -cos a tan ( 180 + a ) = tan a cot ( 180 + a )= cot a |
sin ( 270 - a ) = -cos a cos ( 270 - a ) = -sin a tan ( 270 - a ) = cot a cot ( 270 - a )= tan a | sin ( 270 + a ) = -cos a cos ( 270 + a ) = sin a tan ( 270 + a ) = -cot a cot ( 270 + a )= -tan a |
sin ( 360 - a ) = -sin a cos ( 360 - a ) = cos a tan ( 360 - a ) = -tan a cot ( 360 - a )= -cot a | sin ( 360 . k + a ) = sin a cos (360 . k + a ) = cos a tan ( 360 . k + a ) = tan a cot ( 360 . k + a )= cot a |
kelihatannya susah untuk dihafal, tapi ada cara mudah untuk menghafal :
untuk sudut 90 ± a dan 270 ± a, berubah
(misal : sin menjadi cos, cos menjadi sin, tan menjadi cot )
untuk sudut 180 ± a dan 360 ± a, tetap
( misal : sin menjadi sin, cos menjadi cos, tan menjadi tan )
Bagaimana jika sudutnya negatif, misalnya sin (-a) ?
seperti pada tabel di atas, ( perhatikan tabel baris ke-4 kolom ke-1 )
sudut ( 360 - a ) sama artinya dengan sudut ( -a )
dalam trigonometri sudut yang digunakan biasanya dalam bentuk derajat atau radian
Sekian dulu tentang trigonometri bagian 1, materi selanjutnya akan saya bahas lain waktu. Yang penting banyak latihan soal dan jangan cepat putus asa.
Bersambung...


.gif)
No comments :
Post a Comment