Nih ak posting lagi seputar omits'12
Mau dokumentasi lagi nih
Maaf, cuma daftar nilai ini saja yang bisa saya berikan. Mungkin daftar nilai lainnya menyusul di lain waktu
Karena saya salah satu peserta OMITS'12 SMA, tentunya baru daftar nilai ini saja yang saya posting
Mohon maaf apabila saya tidak bisa memberikan daftar pemenang lomba OMITS'12 karena saya tidak lolos ke final. Jadi saya tidak tahu siapa pemenang omits'12 nya.
Yang ingin melihat-lihat, tidak perlu ragu, langsung saja klik link di bawah ini
DAFTAR NILAI SEMIFINALIS OMITS SMA.doc
Sunday, February 19, 2012
Wednesday, February 15, 2012
Peringkat Nasional Peserta OMITS 12
saya posting kembali info tentang OMITS'12
Bagi anda yang ikut OMITS 12 yang lolos semifinal ataupun tidak tapi belum tahu anda peringkat berapa, atau yang ingin sekedar tahu, anda bisa check di blog saya.
Walaupun sudah ada di website omits, saya ingin mendokumentasikan file ini di blog supaya menjadi kenang-kenangan. Hehe...
Yang ingin lihat, silahkan klik link di bawah ini
SD
SMP
SMA
WEB
Bagi anda yang ikut OMITS 12 yang lolos semifinal ataupun tidak tapi belum tahu anda peringkat berapa, atau yang ingin sekedar tahu, anda bisa check di blog saya.
Walaupun sudah ada di website omits, saya ingin mendokumentasikan file ini di blog supaya menjadi kenang-kenangan. Hehe...
Yang ingin lihat, silahkan klik link di bawah ini
SD
SMP
SMA
WEB
Sunday, February 12, 2012
Trigonometri part 1
Materi trigonometri merupakan salah satu materi membingungkan dalam pelajaran matematika. Memang kesulitan dalam mengerjakan soal trigonometri pasti ada. Mengerjakan soal trigonometri terkadang cepat, terkadang lambat. Rumus saja tidaklah cukup untuk mengerjakan soal trigonometri, kita butuh IDE, bagaimana langkah yang kita ambil selanjutnya. Untuk mendapatkan ide tidaklah mudah, butuh banyak pengalaman seperti banyak latihan mengerjakan soal-soal trigonometri.
maka dari itu janganlah cepat putus asa dalam mengerjakan soal terutama trigonometri, karena putus asa tidak dapat membuat anda sukses.
Kita lanjut ke materi trigonometri
Yang perlu diingat adalah IDENTITAS TRIGONOMETRI
1. sin 2 x + cos2 x = 1
2. 1 + tan2 x = sec2 x
3. 1 + cotan2 x = cosec2 x tinggal tambah awalan co- saja. Tidak perlu susah-susah.
kemudian hubungan antara sin cos tan dengan cosec sec cotan
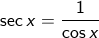 boleh ditulis cosec x
boleh ditulis cosec x
kemudian hubungan antara sin cos tan dengan cosec sec cotan
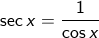 boleh ditulis cosec x
boleh ditulis cosec xboleh ditulis cotan x atau ctg x
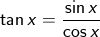.gif)
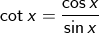.gif)
karena tan x merupakan kebalikan atau invers dari cot x
Sekarang bagaimana cara menghafal sudut-sudut yang berelasi ?
sin ( 90 - a ) = cos a cos ( 90 - a ) = sin a tan ( 90 - a ) = cot a cot ( 90 - a )= tan a | sin ( 90 + a ) = cos a cos ( 90 + a ) = -sin a tan ( 90 + a ) = -cot a cot ( 90 + a )= -tan a |
sin ( 180 - a ) = sin a cos ( 180 - a ) = -cos a tan ( 180 - a ) = -tan a cot ( 180 - a )= -cot a | sin ( 180 + a ) = -sin a cos ( 180 + a ) = -cos a tan ( 180 + a ) = tan a cot ( 180 + a )= cot a |
sin ( 270 - a ) = -cos a cos ( 270 - a ) = -sin a tan ( 270 - a ) = cot a cot ( 270 - a )= tan a | sin ( 270 + a ) = -cos a cos ( 270 + a ) = sin a tan ( 270 + a ) = -cot a cot ( 270 + a )= -tan a |
sin ( 360 - a ) = -sin a cos ( 360 - a ) = cos a tan ( 360 - a ) = -tan a cot ( 360 - a )= -cot a | sin ( 360 . k + a ) = sin a cos (360 . k + a ) = cos a tan ( 360 . k + a ) = tan a cot ( 360 . k + a )= cot a |
kelihatannya susah untuk dihafal, tapi ada cara mudah untuk menghafal :
untuk sudut 90 ± a dan 270 ± a, berubah
(misal : sin menjadi cos, cos menjadi sin, tan menjadi cot )
untuk sudut 180 ± a dan 360 ± a, tetap
( misal : sin menjadi sin, cos menjadi cos, tan menjadi tan )
Bagaimana jika sudutnya negatif, misalnya sin (-a) ?
seperti pada tabel di atas, ( perhatikan tabel baris ke-4 kolom ke-1 )
sudut ( 360 - a ) sama artinya dengan sudut ( -a )
dalam trigonometri sudut yang digunakan biasanya dalam bentuk derajat atau radian
Sekian dulu tentang trigonometri bagian 1, materi selanjutnya akan saya bahas lain waktu. Yang penting banyak latihan soal dan jangan cepat putus asa.
Bersambung...
Saturday, February 11, 2012
Logika Matematika part 1
Logika sangat penting dalam kehidupan kita. Dengan logika, kita lebih efektif dalam mengenal dan menghindari kesalahan penalaran. Salah satu aplikasi logika di bidang rekayasa adalah di bidang teknologi.
Dalam belajar logika matematika, kita perlu tahu yang namanya Pernyataan.
Pernyataan adalah kalimat yang mempunyai nilai kebenaran ( benar / salah, tetapi tidak sekaligus benar dan salah )
Bandingkan 3 pernyataan berikut :
1. Bilangan prima yang genap adalah 2
2. Rumahku jauh dari rumah Dannis
3. 3 lebih besar dari 4
Pernyataan (1) merupakan pernyataan yang bernilai benar karena 2 merupakan satu-satunya bilangan prima yang genap
Pernyataan (2) bukan pernyataan, karena jauh bersifat relatif. Mungkin ada orang yang berpendapat rumahku jauh dari rumah Dannis, tapi pada saat yang sama ada yang beranggapan rumahku tidak jauh dari rumah Dannis
Pernyataan (3) merupakan pernyataan yang bernilai salah. Seharusnya 3 lebih kecil dari 4.
Selain itu ada yang namanya Kalimat Terbuka. yaitu kalimat yang belum dapat ditentukan nilai kebenarannya karena masih memuat variabel.
contoh : 3x + 4 = 10
kalimat tersebut bernilai benar jika x = 2, sedangkan bernilai salah jika x selain 2.
Selanjutnya kita beralih ke pernyataan majemuk ( Konjungsi, Disjungsi, Implikasi, Bimplikasi )
Kunci untuk mengingat
Konjungsi ( kolom 3 ) : bernilai benar jika keduanya benar. selain itu salah
{ .... dan ... }
Disjungsi ( kolom 4 ) : bernilai salah jika keduanya salah, selain itu benar
{... atau ... }
Implikasi ( kolom 5 ) : bernilai salah jika p = benar dan q = salah. selain itu benar
{ jika ... maka ... }
Bimplikasi ( kolom 6 ) : bernilai benar jika kedua pernyataan itu benar atau salah
{ ... jika dan hanya jika ...}
Dalam mengingat tanda konjungsi dan disjungsi biasanya terbalik, lupa...
Cara saya dalam mengingat itu : ambil huruf sebagai kata kunci untuk mengingat
contoh : konjungsi ( DAN ), disjungsi ( ATAU )
Sekian dulu tentang logika math, materi selanjutnya akan diposting lain waktu
Bersambung....
Dalam belajar logika matematika, kita perlu tahu yang namanya Pernyataan.
Pernyataan adalah kalimat yang mempunyai nilai kebenaran ( benar / salah, tetapi tidak sekaligus benar dan salah )
Bandingkan 3 pernyataan berikut :
1. Bilangan prima yang genap adalah 2
2. Rumahku jauh dari rumah Dannis
3. 3 lebih besar dari 4
Pernyataan (1) merupakan pernyataan yang bernilai benar karena 2 merupakan satu-satunya bilangan prima yang genap
Pernyataan (2) bukan pernyataan, karena jauh bersifat relatif. Mungkin ada orang yang berpendapat rumahku jauh dari rumah Dannis, tapi pada saat yang sama ada yang beranggapan rumahku tidak jauh dari rumah Dannis
Pernyataan (3) merupakan pernyataan yang bernilai salah. Seharusnya 3 lebih kecil dari 4.
Selain itu ada yang namanya Kalimat Terbuka. yaitu kalimat yang belum dapat ditentukan nilai kebenarannya karena masih memuat variabel.
contoh : 3x + 4 = 10
kalimat tersebut bernilai benar jika x = 2, sedangkan bernilai salah jika x selain 2.
Selanjutnya kita beralih ke pernyataan majemuk ( Konjungsi, Disjungsi, Implikasi, Bimplikasi )
p | q | ||||
B | B | B | B | B | B |
B | S | S | B | S | S |
S | B | S | B | B | S |
S | S | S | S | B | B |
Kunci untuk mengingat
Konjungsi ( kolom 3 ) : bernilai benar jika keduanya benar. selain itu salah
{ .... dan ... }
Disjungsi ( kolom 4 ) : bernilai salah jika keduanya salah, selain itu benar
{... atau ... }
Implikasi ( kolom 5 ) : bernilai salah jika p = benar dan q = salah. selain itu benar
{ jika ... maka ... }
Bimplikasi ( kolom 6 ) : bernilai benar jika kedua pernyataan itu benar atau salah
{ ... jika dan hanya jika ...}
Dalam mengingat tanda konjungsi dan disjungsi biasanya terbalik, lupa...
Cara saya dalam mengingat itu : ambil huruf sebagai kata kunci untuk mengingat
contoh : konjungsi ( DAN ), disjungsi ( ATAU )
Sekian dulu tentang logika math, materi selanjutnya akan diposting lain waktu
Bersambung....
Ilusi mata
Mata kita digunakan untuk melihat, salah satunya melihat sebuah gambar. Terkadang mata kita dapat tertipu oleh gambar
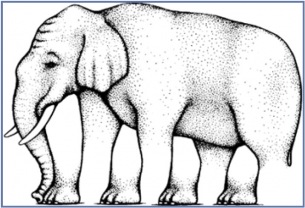
Berikut ini saya hadirkan gambar-gambar yang dapat menipu mata anda,
semua ini hanyalah ILUSI mata anda saja
ini bukan animasi gif. ,melainkan gambar biasa yang formatnya jpg.






Kalau anda jeli, sebenarnya garisnya gak bengkok
Selanjutnya, gambar di bawah ini juga akan membuat anda pusing


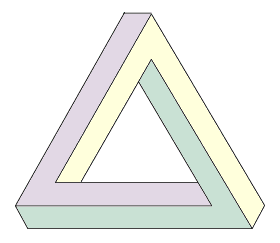
Berikut ini saya hadirkan gambar-gambar yang dapat menipu mata anda,
semua ini hanyalah ILUSI mata anda saja
ini bukan animasi gif. ,melainkan gambar biasa yang formatnya jpg.






Kalau anda jeli, sebenarnya garisnya gak bengkok
Selanjutnya, gambar di bawah ini juga akan membuat anda pusing




Thursday, February 9, 2012
Soal OSN Matematika SMA 2011
Nih aku posting lagi....
walaupun sudah banyak posting tentang soal osn 2011, tidak ada salahnya saya memposting soal osn di blog saya kan?? siapa tau yang belum dapat soal OSN SMA tahun lalu, bisa berkunjung ke sini, untuk bisa menjadi Tim Olimpiade Matematika Indonesia...... Amiiiinnn....
Ini dia. Downloadnya di bawah ini...
soal olimpiade matematika tingkat kabupaten/kota SMA 2011 tipe 1 tipe 3
pembahasan soal olimpiade matematika tingkat kabupaten/kota SMA2011 tipe 1 tipe 3
soal olimpiade matematika provinsi SMA 2011
pembahasan soal olimpiade matematika provinsi SMA 2011
soal olimpiade matematika nasional SMA 2011
pembahasan soal olimpiade matematika nasional SMA 2011
walaupun sudah banyak posting tentang soal osn 2011, tidak ada salahnya saya memposting soal osn di blog saya kan?? siapa tau yang belum dapat soal OSN SMA tahun lalu, bisa berkunjung ke sini, untuk bisa menjadi Tim Olimpiade Matematika Indonesia...... Amiiiinnn....
Ini dia. Downloadnya di bawah ini...
soal olimpiade matematika tingkat kabupaten/kota SMA 2011 tipe 1 tipe 3
pembahasan soal olimpiade matematika tingkat kabupaten/kota SMA2011 tipe 1 tipe 3
soal olimpiade matematika provinsi SMA 2011
pembahasan soal olimpiade matematika provinsi SMA 2011
soal olimpiade matematika nasional SMA 2011
pembahasan soal olimpiade matematika nasional SMA 2011
Wednesday, February 8, 2012
Cara membuat grafik fungsi
Kalau membuat grafik fungsi biasanya kita buatnya di kertas / buku pake penggaris sama pensil atau pulpen. Kita perlu buat koordinat cartesius dulu, baru tentukan titik2 yang ada, dan terakhir tarik garis dari titik2 tersebut.
Nah sekarang, bagaimana caranya buat grafik fungsi di komputer ?
Salah satu caranya dengan menggunakan software tertentu.
Disini saya menyediakan Geogebra

Geogebra merupakan software khusus untuk membuat suatu grafik fungsi. Geogebra merupakan software yang gratis, dapat dijalankan pada komputer yang juga didalamnya telah diinstall java. Jika belum ada Java di komputer anda, maka Geogebra akan meminta anda menginstall Java terlebih dulu
Geogebra dapat digunakan untuk membuat fungsi seperti fungsi linear, kuadrat, hingga fungsi trigonometri. Terlebih dahulu anda memasukkan fungsinya
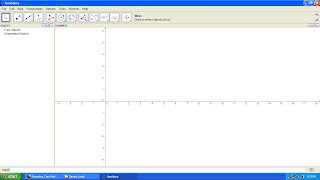
Jika penasaran ingin menggunakannya, silahkan Download saja disini
Nah sekarang, bagaimana caranya buat grafik fungsi di komputer ?
Salah satu caranya dengan menggunakan software tertentu.
Disini saya menyediakan Geogebra

Geogebra merupakan software khusus untuk membuat suatu grafik fungsi. Geogebra merupakan software yang gratis, dapat dijalankan pada komputer yang juga didalamnya telah diinstall java. Jika belum ada Java di komputer anda, maka Geogebra akan meminta anda menginstall Java terlebih dulu
Geogebra dapat digunakan untuk membuat fungsi seperti fungsi linear, kuadrat, hingga fungsi trigonometri. Terlebih dahulu anda memasukkan fungsinya

Jika penasaran ingin menggunakannya, silahkan Download saja disini
Kira-kira bilangan ini termasuk bilangan prima atau gak ya?
Bilangan prima merupakan bilangan yang terdiri dari 2 faktor. yaitu 1 dan bilangan itu sendiri.
Tidaklah mudah untuk mengetahui apakah bilangan itu prima atau bukan. Mungkin, hanya bilangan prima dari 1 sampai 100 saja yang kita hafal. Tetapi masih banyak bilangan prima yang lebih dari 100. Oleh karena itu, bagaimana cara kita mengetahuinya ?
Salah satunya dengan menggunakan suatu program khusus. Setelah searching, akhirnya saya temukan program untuk mencari bilangan prima. Programnya tidak membutuhkan memory yang besar. hanya 386 kb saja. Mudah, ringan, cepat. Pas digunakan untuk belajar......
kalau ingin download, silahkan klik link Disini
Tidaklah mudah untuk mengetahui apakah bilangan itu prima atau bukan. Mungkin, hanya bilangan prima dari 1 sampai 100 saja yang kita hafal. Tetapi masih banyak bilangan prima yang lebih dari 100. Oleh karena itu, bagaimana cara kita mengetahuinya ?
Salah satunya dengan menggunakan suatu program khusus. Setelah searching, akhirnya saya temukan program untuk mencari bilangan prima. Programnya tidak membutuhkan memory yang besar. hanya 386 kb saja. Mudah, ringan, cepat. Pas digunakan untuk belajar......
kalau ingin download, silahkan klik link Disini
Logaritma
Apa yang pertama kali anda pikirkan setelah mendengar kata logaritma ?
Ketika baru pertama kali belajar tentang logaritmadi SMA kelas X, anda pasti merasa bingung. Beberapa siswa SMA merasakan hal yang demikian
Logaritma merupakan Kebalikan ( Invers ) dari Perpangkatan
Konsep Hubungan Logaritma dengan perpangkatan sebenarnya cukup sederhana
ac = b , a log b = c dengan a > 0 , a ≠ 1, b > 0
Keterangan : a = bilangan pokok , b = numerus , c = hasil logaritma
Meskipun kelihatan sederhana, masih banyak siswa SMA yang kesulitan dalam menghafal.
Yang perlu diingat :
Sebelum membahas lebih jauh, adakalanya kita mengetahui sifat-sifat logaritma
Pengurangan Logaritma
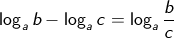
sifat ini berlaku juga jika logaritma yang dikurangkan lebih dari 2
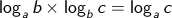 sifat ini berlaku juga jika logaritma yang dikalikan lebih dari 2
sifat ini berlaku juga jika logaritma yang dikalikan lebih dari 2
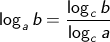
untuk c ≠ 1
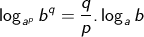
karena p = 1
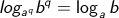 karena q / q = 1
karena q / q = 1
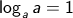 karena a pangkat 1 = a
karena a pangkat 1 = a
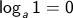
karena a pangkat 0 = 1
Sekian dulu pembahasan tentang logaritma, Soal - soal tentang logaritma saya akan bahas nanti di lain waktu.
Semoga bermanfaat!!!
Ketika baru pertama kali belajar tentang logaritmadi SMA kelas X, anda pasti merasa bingung. Beberapa siswa SMA merasakan hal yang demikian
Logaritma merupakan Kebalikan ( Invers ) dari Perpangkatan
Konsep Hubungan Logaritma dengan perpangkatan sebenarnya cukup sederhana
ac = b , a log b = c dengan a > 0 , a ≠ 1, b > 0
Keterangan : a = bilangan pokok , b = numerus , c = hasil logaritma
Meskipun kelihatan sederhana, masih banyak siswa SMA yang kesulitan dalam menghafal.
Yang perlu diingat :
- Logaritma yang tidak ada bilangan pokoknya seperti log 17, log 293, log 99, dll artinya bilangan pokoknya adalah 10.
- Anda boleh menulis logaritma seperti a log b atau log a b karena keduanya sama
- Dalam menulis logaritma, a log b berbeda dengan a log b karena a log b memiliki bilangan pokok yaitu a, sedangkan a log b memiliki bilangan pokok yaitu 10 dan a log b memiliki arti a kali log b
Sifat-sifat Logaritma
Penjumlahan Logaritma
Pengurangan Logaritma
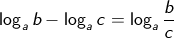
sifat ini berlaku juga jika logaritma yang dikurangkan lebih dari 2
Perkalian Logaritma
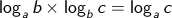 sifat ini berlaku juga jika logaritma yang dikalikan lebih dari 2
sifat ini berlaku juga jika logaritma yang dikalikan lebih dari 2
Sifat logaritma yang lain
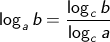
untuk c ≠ 1
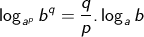
karena p = 1
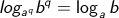 karena q / q = 1
karena q / q = 1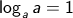 karena a pangkat 1 = a
karena a pangkat 1 = a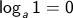
karena a pangkat 0 = 1
Sekian dulu pembahasan tentang logaritma, Soal - soal tentang logaritma saya akan bahas nanti di lain waktu.
Semoga bermanfaat!!!
Tuesday, February 7, 2012
Peserta Semifinal OMITS 12
Subscribe to:
Comments
(
Atom
)


.gif)
.gif)
.gif)













